Benutzer-Werkzeuge
Inhaltsverzeichnis
Ein paar Dinge, die man über Pulsare und deren Beobachtung wissen sollte
Dieser Artikel basiert auf einer Ausarbeitung von Steve Olney. . Sie wurde ausschnittsweise übersetzt und bearbeitet von Wolfgang Herrmann.
Bevor man versucht, Pulsare zu beobachten, ist es sinnvoll, sich ein Bild davon zu machen was für Signale man von einem Pulsar erwarten kann und was das an Herausforderunen für die Beobachtungen bedeutet.
Die Information hier soll nicht eine umfassende Darstellung der Eigenschaften von Pulsaren geben. Es werden lediglich die ganz wesentlichen Aspekte angesprochen. Für ein vertieftes Verständnis ist Google ist dein Freund! Lerne so viel wie möglich über Pulsare und deren Eigenschaften. Einige gute Seiten im Internet hierzu sind:
Es gibt eine Menge Dinge zu lernen. Manche Details mögen eine Herausforderung darstellen, aber gerade dieses macht das Thema so interessant. Ohne ein Verständnis der grundlegenden Prinzipien wird der Versuch einer Detektion schwierig. Schlimmer noch, es könnten Resultate fehlinterpretiert werden und als valide betrachtet werden, die es gar nicht sind.
Wann man ernsthaft in die Materie einsteigen möchte, empfehle ich das „Handbook of Pulsar Astronomy“ von D. Lorimer & M. Kramer. Es ist ein unverzichtbar Begleiter, um etwas über Pulsare und deren Beobachtung zu lernen. Ein Inhaltsverzeichnis des „Handbook of Pulsar Astronomy“ ist hier (als PDF) zu finden.
Allgemeine Signaleigenschaften
Das Signal eines Pulsars ist im Wesentlichen ein Puls breitbandigen Rauschens mit einem typischen Puls- zu Pausenverhältnis von 5%. Es wiederholt sich mit Perioden zwischen mehr als 20 Sekunden und bis zu unter 1,4 ms. Pulare mit einem kleinen Tastverhältnis bei gleicher Gesamtintensität sind leichter zu detektieren, da das Signal stärker aus dem Rauschen hervorragt. Das breitbandige Signal eines Pulsars kann von einigen 10 MHz bis in den Mikrowellenbereich reichen. Da die Radiostrahlung durch einen Synchroton-Mechanismus erzeugt wird, ist das Signal bei niedrigeren Frequenzen bis herunter zu etwa 300 MHz stärker als oberhalb. Noch weiter „unten“ ist es dann wieder schwächer.
Stärke von Pulsarsignalen
Es ist wenig überraschend, dass der erste Parameter, der betrachtet werden muss, die Signalstärke von Pulsaren ist. Die Signalstärke wird ausgedrückt durch die Flussdichte und wird in Jansky gemessen. Diese Einheit ist nach Karl Guthe Jansky benannt, einem amerikanischen Ingenieur der Funktechnik, der als Erster die Emission von Radiowellen aus der Milchstraße entdeckt hat.
Das Jansky (Symbol Jy) ist eine nicht-SI-Einheit der spektralen Flussdichte und entspricht 10−26 Watt pro Quadratmeter und Hertz.
Ein Anhaltspunkt, was das bedeutet: Wenn man die Energie einer Quelle mit 1 Jansky mit der derzeit größten Antenne (FAST: 500 m Durchmesser) und einer Bandbreite von 1 GHz (die derzeit maximale Bandbreite von FAST) einsammelt, dann bekommt man lediglich 2 x 10-12 Watt. Die gilt unter den Annahme, dass man tatsächlich die gesamte aufgefangene Energie auch auffangen kann. Dann braucht man 16.000 Jahre um eine Glühbirne mit 1 Watt Leistung eine Sekunde lang zu betreiben! Hat man hingegen eine typisches Amateurausrüstung (mal angenommen eine 10 m Schüssel mit einer Effizienz von 70% und 10 MHz Bandbreite), dann braucht es 5.000 Millionen Jahre um die Energie zu bekommen, um eine 1 Watt Glühbirne 1 Sekunde lang zu betreiben.
Nun hat nur der Vela Pulsar eine Flussdichte von deutlich mehr als 1 Jy, nämlich 5 Jy bei 400 MHz. Diese Tabellen zeigen die Flussdichte von verschiedenen Pulsaren in absteigender Reihenfolge, und da sind wir in den allermeisten Fällen unterhalb von 1 Jansky. Wie man sieht, nimmt die Flussdichte nach den ersten beiden Pulsaren rapide ab. Daher sind üblicherweise die ersten Kandidaten für eine Detektion der B0329+54 für die nördliche Hemisphäre und der B0833-45 (Vela Pulsar) für die südliche Hemisphäre.
Erstaunlicherweise ist der erste Pulsar, der von Jocelyn Bell im Jahr 1967 entdeckt wurde, keineswegs der stärkste. Dieser Pulsar, B1919+21 genannt, ist mit einer Flussdichte von 57 mJy bei 400 MHz bzw. 6 mJy bei 1400 MHz zu schwach um mit Amateurmitteln beobachtet zu werden.
Antennenfläche, Bandbreite und Beobachtungszeit
Wie erwähnt, beschreibt die Einheit Jansky die Leistung pro Quadratmeter und Hertz. Um also mehr Energie vom Pulsar zu empfangen, kann man also sowohl eine größere Empfangsfläche als auch eine größere Bandbreite verwenden. Die letztere Option erfordert aber bei höheren Bandbreiten eine komplexe Signalverarbeitung. Dies liegt an der sogenannten Dispersion, die dazu führt dass die Ausbreitungsgeschwindigkeit frequenzabhängig ist. Dummerweise nimmt die Verzögerung bei niedrigeren Frequenzen (also gerade dort wo der Pulsar am stärksten ist) signifikant zu. Wenn die gewählte Bandbreite zu groß ist, dann wird der Puls „verschmiert“ und ist entsprechend schwerer zu detektieren. Man kann sich vorstellen, dass wenn die Verzögerung so groß wie die Pulsperiode ist, das Signal ganz verschwindet. Wie man diesen Effekt kompensieren kann, ist weiter unten unter „Dispersion“ erläutert.
Es wundert daher nicht, dass es am Besten ist, eine möglichst große Empfangsfläche zu verwenden. Natürlich kann man auch die Empfindlichkeit dadurch steigern, dass man länger beobachtet. Auch das stößt jedoch an Grenzen: Reduziert man beispielsweise den Antennendurchmesser von 6m auf 3m, geht die Empfangsfläche auf ein Viertel zurück und man muss 16 mal so lange beobachten, um wieder die gleiche Empfindlichkeit zu erhalten. Glücklicherweise kann man Bandbreite und Beobachtungszeit kombinieren: Der Faktor 16 kann durch 4-fache Bandbreite und 4-fache Beobachtungszeit erreicht werden.
Dispersion
Auf dem Weg vom Pulsar zum Empfänger auf der Erde läuft das Signal durch das interstellare Medium (ISM). Einer der dabei auftretenden Effekte ist die Dispersion. Im wesentlichen führt dies dazu, dass Signale mit niedriger Frequenz später ankommen als Signale mit höherer Frequenz. Bei Pulsaren beginnt die Reise für alle Frequenzen zum gleichen Zeitpunkt. Auf dem Weg zur Erde werden die verschiedenen Frequenzkomponenten unterschiedlich verzögert, was zu einem merklichen Zeitunterschied zwischen niedrigen und hohen Frequenzen führt.
Je nach Pulsar ist dieser Effekt unterschiedlich: Die Entfernung zum Pulsar und das interstellare Medium unterscheidet sich jeweils. So hat jeder Pulsar seine eigene Dispersions-Charakteristik, die als „Dispersion Measure (DM) bezeichnet wird.
Die Näherungsgleichung für den Fall, dass der Frequenzunterschied f1 - f2 klein gegenüber der Empfangsfrequenz ist, lautet
Δtdisp = 4,15 * 106 * (f1-2 - f2-2 ) * DM
wobei hier der Zeitunterschied in Millisekunden und die Frequenzen in MHz angegeben sind.
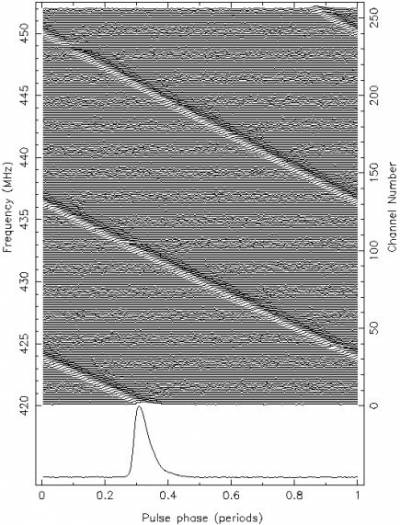
Die Auswirkung dieses Effektes ist, dass der Pulse verschmiert wird, wenn über eine größere Bandbreite beobachtet wird. Die Signale bei unterschiedlichen Frequenzen liegen zeitlich nicht genau übereinander, und das Signal/Rauschverhältnis ist schlechter. Ein Puls mit schmaler Pulsbreite ist naturgemäß stärker betroffen als ein breiterer Puls. Das nachstehende Bild zeigt diesen Effekt am Beispiel des Vela Pulsars bei einer Empfangsfrequenz um 435 MHz:
Um diesem Effekt zu begegnen, wird ein Prozess auf die gewonnenen Daten angewandt, der sich De-Dispersion nennt. Dabei unterscheidet man zwischen „kohärenter De-Dispersion“ und „inkorhärenter De-Dispersion“. Bei der ersteren wird ein Filter angewandt, dessen Eigenschaften genau das inverse der Phasenverzögerung der intestellaren Materie darstellen. Inkohärente De-Dispersion ist das Verfahren, bei der das Signal in einzelne Frequenbänder aufgeteilt wird und dann auf jedes Frequenzband eine Zeitverzögerung angewandt wird, um den Effekt der Interstellaren Materie zu kompensieren. Diese Methode ist „ungenauer“ und stellt das ursprüngliche Signal nicht so perfekt wieder her. Dafür ist sie einfacher zu implementieren.
Szintillation
Die Flussdichte von Pulsaren wird durch einen Effekt beeinflusst, der als Szintillation bezeichnet wird. Szintillation kann die Stärke zeitweise deutlich anheben, und zu anderen Zeiten kann sie so stark herabgesetzt sein, dass der Pulsar nicht beobachtet werden kann. Wie stark die Szintillation ausgeprägt ist und und in welchen Zeiträumen sie sich abspielt ist von Pulsar zu Pulsar recht unterschiedlich. Gerade bei dem für den Amateur in der nördlichen Hemisphäre interessanten Pulsar B0329+54 ist sie recht signifikant.
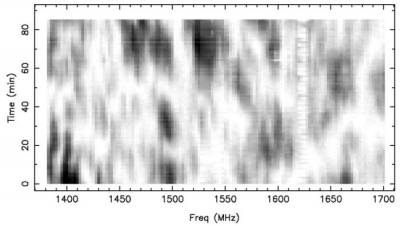
Das nachstehende Bild zeigt die Variation der Signalstärke in einem Zeitraum von 85 Minuten im Frequenzbereich von rund 1400 bis 1700 MHz. Die Stärke der Graufärbung stellt dabei die Stärke des Signals dar:
Wie man erkennen kann, ist das Signal zu bestimmten Zeiten verstärkt, und zu anderen Zeiten deutlich vermindert. Das bedeutet, dass man je nach Beobachtungsfrequenz und -bandbreite und Zeitpunkt der Beobachtung sehr unterschiedliche Ergebnisse erzielen kann. In der Praxis bedeutet dies, dass mal eine Beobachtung gelingt und zu anderen Zeiten eben nicht.
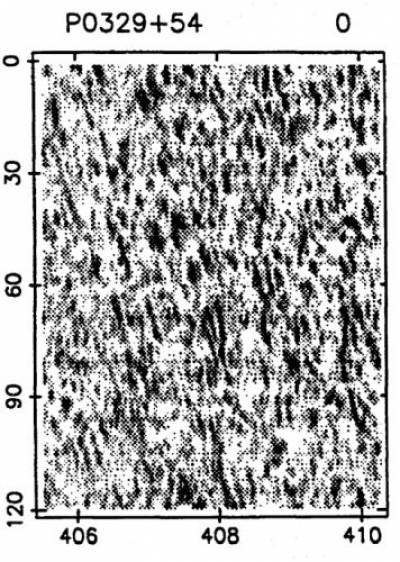
Zu beachten ist weiterhin, dass das Szintillationsverhalten in anderen Frequenzbereichen anders ausfallen kann. Bei niedrigeren Frequenzen spielt sich die Szintillation beim gleichen Pulsar B0329+54 auf sehr viel kleineren Frequenz- und Zeitskalen ab:
Hier wird man also recht konstante Resultate erzielen. Anderseits hat man aber auch nicht den Vorteil, mal einen „glücklichen Moment“ zu erwischen.
Doppler Effekt
In Berichten über Pulsaren wird immer herausgehoben, dass ihre Wiederholrate oder Pulsarfrequenz außerordentlich stabil ist und z.T. die Stabilität von Atomuhren übertrifft. Dies ist richtig, wird aber von einem Effekt überlagert: Wenn wir auf der Erde einen Pulsar beobachten, dann tun wir dies nicht von einem ruhenden System aus. Unsere Erde bewegt sich um die Sonne, dreht sich um sich selber und wird auch noch von weiteren Effekten wie der Schwerkraft des Mondes und der anderen Planeten beeinflusst. Dadurch bewegen wir uns je nach Zeitpunkt der Beobachtung mit unterschiedlicher Geschwindigkeit gegenüber dem Pulsar. Entsprechend wird die Pulsarfrequenz dopplerverschoben sein. Man unterscheidet daher zwischen der „barizentrischen“ und „topozentrischen“ Pulsarfrequenz. Die erste ist auf das Schwerpunktzentrum des Sonnensystems bezogen und in der Tat außerordentlich konstant. Die zweite ist hingegen auf den Ort der Beobachtung bezogen und unterliegt den Schwankungen durch die Bewegung des Beobachters. In den Katalogen wie z.B. im ATNF Pulsar Katalog ist immer die barizentrische Periode angegeben.
Spin Down
Wenn auch die Pulsarperiode sehr konstant ist, so ist sie doch nicht unveränderlich. Der Pulsar verliert durch Abstrahlung fortlaufend an Energie, und dadurch nimmt seine Rotationsgeschwindigkeit ab. Dieser Prozess ist zwar gering, spielt aber doch eine Rolle bei der Beobachtung. Wenn man also eine Rotationsperiode bei der Messung unterstellt, sollte sie daher aktuell sein.